这篇文章只是一些对论文的总结,以便看起来容易理解一点,可能有点翻译腔,大概看得懂就行
原论文链接NEUZZ: Efficient Fuzzing with Neural Program Smoothing
introduction
由于其简单和低额外开销,fuzz在发现真实应用漏洞中取得了很大的成就。虽然很多fuzzer都声称自己能有非常好的效果,但是很多时候,特别在面对大型程序的时候,经常陷入不断尝试冗余无效的测试样例,艰难地想寻找应用漏洞的困境中
理论上来说,fuzzing是一个最优化问题,这个问题的目标就是在一定时间内,找到一些程序输入使得其发现的程序漏洞尽可能的多,但是一般来说,程序中的安全问题是非常稀有且不规律的分布在程序代码之中。大部分的fuzzer目标就是提高输入的代码覆盖率,去增加找到安全漏洞的几率。大部分现代的fuzzer使用进化算法去解决一个基础优化问题——生成新的输入使得其代码覆盖率最大化。进化算法从一堆种子输入开始,随机突变这些种子来生成新的测试输入,用这些新的测试数据来输入到目标程序中,并且只留下那些能发现未覆盖代码的测试数据。但是,当输入的语料库变大的同时,进化的过程变慢(指的是覆盖到新的代码区域)
对于进化算法的一个限制就是,它们不能利用基础最优化问题来获得更好效果。 而Gradient-guided最优化算法是一种非常有前途的方法,在很多不同的领域如 空气动力学计算,机器学习上,取得了比进化算法好的多的结果。
但是,gradient-guided 最优化算法并不能直接用来fuzz实际应用,因为这些应用经常拥有大量的,不连续的行为(例如case,并不能准确的去计算其梯度),并且应用与应用之间的行为差异非常大。我们发现这个问题可以用一种方法来解决,那就是创造一个平滑的替代函数去大概的模拟目标程序对于不同输入的分支行为(branching behavior)。不幸的是,目前存在的程序平滑化技术都有令人望而却步的性能损耗,因为它们都非常依赖于符号执行,而由于路径爆炸,不完全的环境模拟,符号建模占用大量内存等问题,符号执行并不能扩展到大型程序。
在这篇文章中,我们介绍一种新颖,有效,可扩展的程序平滑技术,这种技术使用前向反馈神经网络,能够逐步学习去平滑地模拟复杂实际应用的分支行为。我们进一步地提出了一种gradient-guided搜索策略,这种策略能利用平滑模拟函数去找到那些能使发现漏洞数最大化的突变位置。我们将会介绍如何使用增量训练,在预测错误的程序行为上,提取出一个NN model(neural network)。我们发现 前向反馈神经网络( feed-forward NNs )非常适用于这个任务,因为它有对于非线性函数的模拟能力,并且能有效而准确地计算出梯度/高阶导数( gradients/higher-order derivatives)
我们利用这个技术实现了 NEUZZ,一个新型可学习的fuzzer。 我们将在………..(大概意思就是,比较了NEUZZ和其他10个fuzzer在实际应用,LAVA-M,CGC中的效果,结果就是NEUZZ比其他fuzzer都优秀很多,并且发现了两个新的CVE)
OPTIMIZATION BASICS
在这个部分,我们首先介绍了最优化问题的基础,以及gradient-guided最优化方法相比于进化算法的优点。最后,我们将会说明如何将fuzzing转化为一个最优化问题。
一个最优化问题一般包含三个不同的部分: a vector of parameters x, an objective function F(x) to be minimized or maximized, and a set of constraint functions Ci(x) each involving either inequality or equality that must be satisfied (这里用英文比较准确)
最优化的目标就是找到parameter vector x 的实际值,使得F(x) 最大化/最小化 同时满足所有 constraint functions Ci(x)
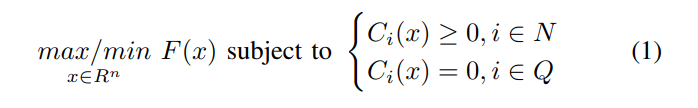
这里 R, N ,Q分别是 是一组实数,inequality constraints的指数,equality constraints的指数
Function smoothness & optimization
最优化问题开始时随机地设置一组变量x,并在迭代中不断地改变x,使其能找到最优解。任何最优化算法的关键就是如何从一组变量x 转变为下一组变量。大部分的策略是利用函数 F,constraint functions Ci,如果可以的话,gradient/higher-order derivatives
不同最优化算法获得最优解的能力和效率非常依赖objective and constraint functions F and C。一般来说,平滑的函数比不连续的函数更容易进行优化。直觉地说,objective/constraint functions越平滑,最优化方法就越容易地计算出梯度或高阶导数,并用他们来去系统性地搜寻整个解/状态空间。
这篇论文剩下的部分,我们将会专注于不受限制的最优化问题,即没有任何限制函数(constraint functions),因为这种最优化问题非常近似于我们的目标,fuzzing。对于不受限的最优化问题,gradient-guided的方法能取得比进化算法好很多的效果。因为gradient-guided的方法有效的利用了梯度/高阶函数去寻找最优解
Convexity & gradient-guided optimization.
对于凸函数,gradient-guided的方法非常有效,并且经常能找到全局最优解。直觉上,如果一个函数是凸函数的话,balabala,大概就是介绍凸函数(https://zh.wikipedia.org/zh-sg/%E5%87%B8%E5%87%BD%E6%95%B0)
然而,对于非凸函数,gradient-guided的方法经常陷入局部最优解,不过,即使是这种情况,也有一种简单的方法来解决,那就是在随机一个点重新开始gradient-guided方法,在实际应用中非常有效。
Fuzzing as unconstrained optimization.
Fuzzing可以表示为一种不受限的最优化问题,这个问题的目标就是对于给定数量的输入,最大化在程序中找到的漏洞。因此目标函数可以表示为 $F_p(x)$,当目标程序使用输入x时触发了一个漏洞,这个函数返回1。然而,这个函数太 ill-behaved 以至于很难去有效的优化。
因此,大部分的灰盒fuzzer使用最大化被测试的代码数量(代码覆盖率等) 作为替代的度量方法。这种目标函数可被表示为
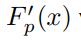
F’ 返回的是对于程序P,输入x触发的新的控制流边数。F’ 比原来的函数F更容易优化,因为触发新的控制流边的输入比触发漏洞的输入要多。
大部分现有的灰盒fuzzer将进化函数和其他特定领域的启发式配合使用,作为主要优化策略。使用这些算法而不是gradient-guided最优化方法的主要原因是大部分的实际应用存在很多不连续性,而这种不连续性在选择不同程序路径时更加明显。这种不连续性会使得gradient-guided最优化方法陷入不是最优的解中。在这篇论文中,我们提出了一种新的技术,使用神经网络来将目标程序平滑化,使其更适合gradient-guided最优化方法,我们将会说明fuzzer如何去exploit这种策略使得其能有效提高效率。
OVERVIEW OF OUR APPROACH
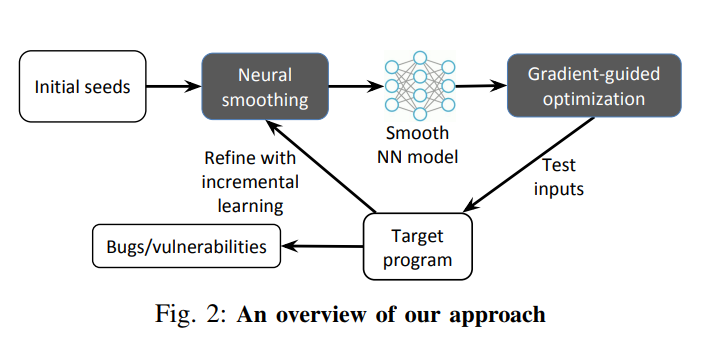
Neural program smoothing.
平滑地逼近/近似/模拟 一个程序的不连续分支行为是准确计算梯度和高阶倒数的关键。如果没用平滑化,那么gradient-guided会因此陷入不同的不连续性中。平滑化过程的目标是创造一个能模仿程序分支行为而不引入较大错误的平滑函数。我们使用前向反馈神经网络来完成这个目标。由通用逼近理论而启发,使用神经网络是用来逼近任意复杂程序行为是非常好的。更进一步。神经网络,在设计上,能高效地计算出对于我们的目标非常关键的梯度。我们将使用现有的测试输入或进化式fuzzer生成的语料库来训练神经网络。
Gradient-guided optimization.
一旦神经网络模型被训练好,可以用来高效地计算出梯度和高阶函数,使用其来更快地找到最优解。有很多种不同的Gradient-guided算法例如梯度下降,Newton’s method,or quasi-Newton methods like the L-BFGS algorithm。Smooth NNs 使得fuzzing测试输出生成程序能有可能使用所有这些技术。在这篇文章中,我们设计,实现,并评估了一种为基于覆盖的fuzzing而量身订造的gradient-guided测试输出生成方法。
Incremental learning.
任何现有类型的测试输入都有可能被用来训练NN model和引导fuzzing测试输出生成过程。在这篇文章中,我们通过收集一堆测试输入和由进化fuzzers如AFL生成的对应的边覆盖信息来训练NN model。
但是,由于训练NN model的初始数据可能只覆盖到程序空间的一小部分,所以我们进一步通过增量训练来训练模型,因为在fuzzing的过程中,新的程序行为可以被观察到。在增量训练中,主要面对的难题是,在训练新的数据的过程中,模型有可能完全忘记从旧数据中学习的规则。为了避免这个问题,我们设计了一种新的基于覆盖的过滤方案,这种方案会生成旧数据和新数据的简练的总结,使得NN model能高效地在其上面训练。
A Motivating Example.
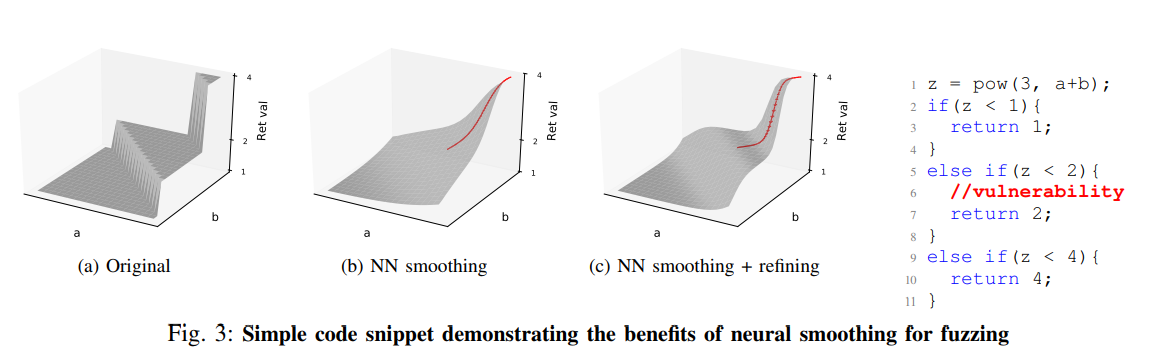
我们在图中大概说明了我们算法的内部大概状况,右边的的一小段c语言代码,它返回不同的值基于计算pow出来的值的范围,我们将假设有漏洞的地方在红色的部分。
考虑这么一种情况,进化式的fuzzer如AFL勉强能探索到第2行和第9行的代码,但是并不能覆盖到第5行的代码。这种情况的关键难点就是a和b的值,使得其能触发到第5行代码。进化式fuzzer通常很难覆盖到这一部分,因为通过随机突变来找到一种解决方案的可能性是非常低的。那段c语言代码可以表示如图3a,在函数平面上, a+b = 0 到 a+b−$\epsilon$ = 0 ($\epsilon$ -> +0) 有一个非常急剧的平面差。为了在fuzzing中最大化边覆盖率,进化式的fuzzer只能依赖于随机突变,但随机突变并没有考虑函数平面的形状。相比之下,我们的
NN平滑和梯度引导的突变被设计为利用梯度来测量函数表面形状。
我们训练一个关于程序行为的NN模型其他两个分支。 NN模型平滑近似程序行为如图3b和3c所示。 然后我们使用NN模型执行更有效的梯度引导优化以找到a和b的期望值
,并逐步细化模型,直到在目标分支上发现漏洞为止。
METHODOLOGY
我们将在这个部分描述了我们的方案的不同组成部分。
A. Program smoothing
程序平滑是使梯度引导优化技术适用于fuzzing 具有离散行为的程序现实世界的重要步骤。没有平滑,梯度引导优化技术不是很有效优化非平滑函数,因为它们往往会陷入在不同的不连续上。
平滑过程使这种不规则性最小化,因此使梯度引导优化在不连续函数上显得更有效。一般来说,不连续函数f的平滑化可以被视为 f和一个平滑mask函数g的卷积生成的一个新的平滑函数。 流行的平滑mask函数有不同的高斯和Sigmoid函数等。
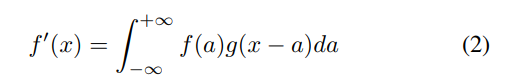
然而,对于许多实际问题,不连续函数f可能不具有封闭形式的表示,因此不可能表示为上述的函数。在这种情况下,我们将会使用离散形式的函数版本进行数值计算。
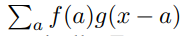
例如,在图像平滑中,通常使用固定大小的2-D卷积核来执行这种计算。但是,在我们的设置中,f是一个计算机程序,因此无法通过分析计算相应的卷积。
程序平滑化可以被分为两类:黑盒平滑化,白盒平滑化。黑盒方法从f的输入空间中选取离散样本,并使用这些样本来计算卷积。而白盒方法,可以查看程序中的代码/指令,并且能使用符号执行和抽象执行来总结他们的效果/影响。黑盒方法可能会引入大量的逼近/近似错误,而白盒方法则可能因为令人望而却步的性能损耗而使其不适用于实际应用。
为了避免这些问题,我们使用NN以灰盒方式来学习平滑化的程序行为,我们将会在下面详细说明。
Neural program smoothing
在这篇文章中,我们提出一个新颖的程序平滑化方法,这种方法使用NN models,基于观察到的程序行为,迭代的学习目标程序的平滑化。这种神经网络可以平滑地推广到观察到的程序行为,同时还准确地建模潜在的非线性和非凸行为。一旦训练完成,神经网络可用于有效地计算梯度和更高级别的导数,以指导模糊输入生成过程,如图3所示。
Why NNs?
正如通用逼近定理所启示的,NN非常适合近似复杂的程序行为。使用NN来平滑化程序的优点有:(1) NN可以准确地模拟复杂的非线性程序行为,并且可以有效地进行训练,之前已经有人使用线性和二次模型来进行模拟。
然而,这些模型不适合用于建模具有高度非线性和非凸性行为的实际软件。(2) NN支持有效计算其梯度和高阶导数。因此,gradient-guided算法可以在fuzzing中计算和使用这些信息,而无需任何额外开销。(3) NN可以概括并学习根据类似输入的行为来预测程序对未知输入的行为,因此,NN可以基于其对少量输入样本的行为来潜在地学习整个程序的平滑近似。
NN Training
虽然NN可以用来模拟程序行为的不同方面,但在本文中我们专门用它们来模拟目标程序的分支行为。使用神经网络对分支行为进行建模的挑战之一是需要接受可变大小的输入。与实际应用不同,前馈NN通常接受固定大小的输入。因此,我们设置最大输入大小阈值,并在训练期间使用空字节填充任何较小尺寸的输入。而支持更大的输入不是主要问题,因为现代NN可以轻松扩展到数百万个参数。因此,对于较大的程序,我们可以根据需要简单地增加阈值大小。然而,我们凭经验发现相对适度的阈值产生最佳结果,而较大的输入不会显着提高建模精度。
正式地,让 $f: ${0x00,0x01,……,0xff}$^m$ -> ${0,1}^n$ NN模型大小为m的字节序列作为输入,并输出大小为n的bitmap。让 $\theta$ 作为 $f$的可训练权值参数。给定一组训练样本$(X,Y)$,X是输入数据,Y是对应的边覆盖bitmap,参数函数$f(x,\theta) = y $ 的训练任务是得到一个参数$\hat{\theta}$,使得最小化
$$\min \sum_{x \in X, y \in Y} L(y,f(x,\theta))$$
$L(y,f(x,\theta))$是NN model的输出和在训练集中真正的 $y \in Y$的损失函数。训练任务就是找到NN $f$的一组权值 $\theta$,使得误差最小化,这个误差使用距离去度量。特别的,我们使用我们使用二进制交叉熵来计算预测bitmap和真实覆盖bitmap之间的距离。还有,我们让$y_i$ 和 $f_i(x,\theta)$来表示真正输出bitmap中第i个bit和预测输出bitmap中第i个bit。然后,这两者之间的二元交叉熵定义为
$$-\frac{1}{n} \sum_{i=1}^n [y_i \cdot \log(f_i(x,\theta))+(1-y_i) \cdot \log(1-f_i(x,\theta)))] $$
在本文中,我们使用前馈完全连接的NN来模拟目标程序的分支行为,使用前馈架构允许高效地计算梯度和快速训练。
我们的平滑技术与训练数据的来源无关,因此可以对从现有输入语料库收集的任何边缘覆盖数据进行NN训练。对于我们的原型实现,我们使用现有的进化模糊器(如AFL)生成的输入语料库来训练我们的初始模型。
Training data preprocessing
由训练数据执行的边缘覆盖通常倾向于偏差,因为它仅包含程序中所有边缘的一小部分的标签。例如,一些边缘可能被训练集中任意一个输入所触发。一组标签之间的这种类型的相关性在机器学习中被称为多重共线性,这通常会阻止模型收敛到一个小的损失值。为了避免这种情况,我们通过将总是一起出现在训练数据中的边缘合并为一个边缘,这是常见机器学习实践方法。此外,我们仅考虑在训练数据中至少激活一次的边缘。通过这几个步骤,使得标签数量从平均65535个下降到大约4000个。不过,我们在每次增量学习迭代时重新运行数据预处理步骤,因此一些合并标签可能会因为在模糊测试期间发现新边缘数据时相关性降低而被拆分。
Gradient-guided optimization
不同的梯度引导优化技术,如梯度下降,牛顿法或准牛顿法,L-BFGS,可以使用梯度或更高阶导数来实现更快的收敛。平滑NN使得模糊输入生成过程可以通过支持梯度和高阶导数的有效计算,使得其能使用这些技术的任意一种。在本文中,我们专门设计了一个简单的梯度引导搜索方案,该方案对于较小的预测误差具有鲁棒性,以证明我们的方法的有效性。我们将会在未来探索更加复杂的工作。
在描述基于NN梯度的变异策略之前,我们首先提供梯度的形式定义,指示每个输入字节应该改变多少以影响NN中最终层神经元的输出(边缘覆盖)。这里每个输出神经元对应一个特定的边缘,并计算一个介于0和1之间的值,判断给定输入字节对特定边缘的影响。NN model输出单元的梯度已被广泛用于对抗性输入生成,以及可视化/理解DNN。直观地,基于梯度的指导的目标是找到将改变对应于从0到1的不同边缘的最终层神经元的输出的输入。
给定在section IV-B中 一个参数化NN $y=f(\theta,x)$ ,让$y_i$表示$f$的最后一层中第i个神经元的输出,也可以写做 $f_i(\theta,x)$。给定特定的输入,$f_i(\theta,x)$ 的梯度$G$可以被定义为 $G = \triangledown_x f_i(\theta,x) = \partial y_i/\partial x $ 。$f’s$ 相对于 $\theta$ 的梯度可以容易的计算出来,而在训练NN的过程中需要不断迭代地更新$\theta$。因此,可以通过简单地计算出$x$相对于$\theta$的偏导,能得到$G$ 。注意,梯度G的维数与输入x的维度相同,在我们的例子中,它是一个字节序列。
伪代码如下

Gradient-guided optimization.
算法1显示了梯度引导输入生成过程的概要。算法的关键思想是识别具有最高梯度值的输入字节并对其进行变异,因为它们表明对NN的重要性更高,因此更有可能导致程序行为发生重大变化。
从种子开始,我们迭代地生成新的测试输入。 如算法1所示,在每次迭代时,我们首先利用梯度的绝对值来识别输入字节,这些输入字节将导致输出神经元对应于未被捕获的边缘的最大变化。接下来,我们检查每个字节的梯度符号,以确定突变的方向来最大化/最小化目标函数。从概念上讲,我们使用渐变符号类似于引入的对抗性输入生成方法。我们还将每个字节的变异限制在其合法范围内(0-255)。 第6行和第10行表示使用clip function来进行限制。我们用一个小的变异目标(算法1中的k)开始输入生成过程,并指数增加要变异的目标字节数,以有效地覆盖大输入空间
Refinement with incremental learning
梯度引导输入生成过程的效率在很大程度上取决于NN如何准确地模拟目标程序的分支行为。为了获得更高的精度,我们在模糊过程中观察到不同的程序行为时,逐步细化NN模型。我们使用增量学习技术通过在触发新边缘时学习新数据来更新NN模型。改进NN model的主要挑战是避免NN模型在训练新数据时突然忘记先前从旧数据中学到的信息。这种遗忘是深度学习文献中众所周知的现象,并被认为是稳定性 - 可塑性困境的结果。为了避免这种遗忘问题,NN必须足够改变权重以学习新任务,但不能过多地使其忘记以前学过的知识。优化NN的最简单方法是将新的训练数据与旧数据一起添加,并再次从头开始训练模型。但是,随着数据量的增加,这种再训练变得更难以扩展。 先前的研究试图主要使用两种广泛的方法来解决这个问题。第一个方法为新旧模型保留单独的表示,以最大限度地减少使用分布式模型,正则化或从多个模型中创建遗忘集合。第二种方法维护旧数据的摘要,并在新数据上重新训练模型以及汇总的旧数据,因此比完全再训练更有效。在本文中,我们使用基于边缘覆盖的过滤来仅保留触发新分支以进行重新训练的旧数据。 随着新的训练数据变得可用,我们确定实现新边缘覆盖的数据,将它们与过滤的旧训练数据放在一起,并重新训练NN。这种方法有效地防止训练数据样本的数量在重新训练迭代次数上急剧增加。我们发现我们的过滤方案可以轻松支持多达50次重新训练,同时仍将训练时间保持在几分钟之内。
IMPLEMENTATION
下面就是实现和评估的细节,这里就不详细翻译了